The Fibonacci sequence: an introduction
The Fibonacci sequence is probably one of the most
famous — and most widely written-about — number sequences in all of
mathematics. So why write about it, if it’s been written about so much
already? Well, because I can, and because it’s fun — there are good
reasons it’s so popular! I plan to spend the next five posts (at least)
talking about the Fibonacci sequence and its connections to other areas
of mathematics.
The Fibonacci sequence is defined by the recurrence relation

In English, this says that the first two Fibonacci numbers are both equal to 1, and any Fibonacci number from the third onwards can be obtained by adding the previous two Fibonacci numbers. So the third Fibonacci number is 1 + 1 = 2; the fourth is 1 + 2 = 3; then 2 + 3 = 5; and so on. The first fifteen Fibonacci numbers are
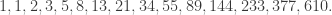
As you can see, they get large fairly quickly. The 31st Fibonacci number is the first to exceed one million, and the 45th is already bigger than one billion.
The definition of the Fibonacci sequence is quite simple, but there’s a LOT more here than meets the eye, which I hope to expand on in subsequent posts. For now, we’ll start with this simple observation: what happens if you sum all the Fibonacci numbers up to a certain point? For example, let’s add up all the Fibonacci numbers up to 5: 1 + 1 + 2 + 3 + 5 = 12. Okay. How about going one further: 1 + 1 + 2 + 3 + 5 + 8 = 20. If we include 13 as well, we get 33. Do you see a pattern? (Hint: compare the sums we got (12,20,33) with the Fibonacci sequence itself.) Does this always work, and if so, can you show why (and if not, can you give an example where it doesn’t)? Feel free to post comments!
The Fibonacci sequence is defined by the recurrence relation
In English, this says that the first two Fibonacci numbers are both equal to 1, and any Fibonacci number from the third onwards can be obtained by adding the previous two Fibonacci numbers. So the third Fibonacci number is 1 + 1 = 2; the fourth is 1 + 2 = 3; then 2 + 3 = 5; and so on. The first fifteen Fibonacci numbers are
As you can see, they get large fairly quickly. The 31st Fibonacci number is the first to exceed one million, and the 45th is already bigger than one billion.
The definition of the Fibonacci sequence is quite simple, but there’s a LOT more here than meets the eye, which I hope to expand on in subsequent posts. For now, we’ll start with this simple observation: what happens if you sum all the Fibonacci numbers up to a certain point? For example, let’s add up all the Fibonacci numbers up to 5: 1 + 1 + 2 + 3 + 5 = 12. Okay. How about going one further: 1 + 1 + 2 + 3 + 5 + 8 = 20. If we include 13 as well, we get 33. Do you see a pattern? (Hint: compare the sums we got (12,20,33) with the Fibonacci sequence itself.) Does this always work, and if so, can you show why (and if not, can you give an example where it doesn’t)? Feel free to post comments!
No comments:
Post a Comment